- Data-Driven Momentum Observers With Physically Consistent Gaussian Processes. IEEE Transactions on Robotics 40, 2024, 1938-1951 mehr… BibTeX
- Physically Consistent Learning of Conservative Lagrangian Systems with Gaussian Processes. 2022 IEEE 61st Conference on Decision and Control (CDC), IEEE, 2022 mehr… BibTeX
Data-driven Control
Classical control approaches are based on physical dynamic models, which are required to describe the true underlying system behaviour in a sufficiently accurate fashion. For complex dynamical systems, however, such descriptions are often extremely hard to obtain or even nonexistent, hence data-driven approaches have to be employed. Data-driven models are based on observations and measurements of the true system and only require a minimum amount of prior knowledge of the system. However, they require new control approaches since classic analysis and synthesis tools are not suitable for models of probabilistic nature. Our work focuses on the Gaussian process model, which is very generally applicable and has shown to be successful in many control scenarios. We develop new control algorithms, which not only improve the overall performance but also guarantee the stability of the closed-loop system. Finally, the approaches are tested and validated in robotic experiments.
Current topics:
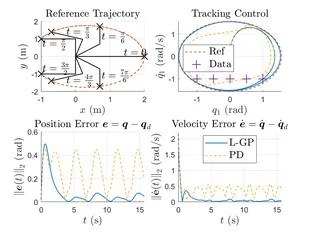
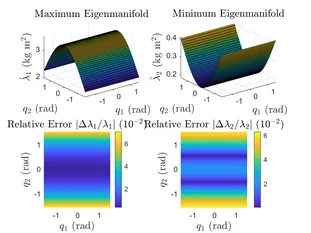
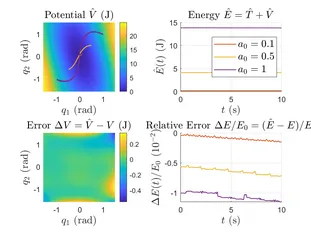
Learning and Control of Physical Systems with Lagrangian-Gaussian Processes
Researcher: Giulio Evangelisti
Motivation
Lagrangian systems comprise a large class of physical systems such as robots, aircrafts or marine vehicles. The application of Gaussian Processes (GPs) in learning-based control has the potential to significantly improve criteria such as performance and safety. However, in general GP regression does not account for key problems such as:
- physical consistency, i.e., the fulfillment of the fundamental underlying physical properties,
- the trade-off between physics-imposed symmetries and model flexibility,
- reliable and robust applicability in the control of uncertain physical/passive systems,
- computational efficiency and data-efficiency.
Approach
Our main approach is to construct & apply physically consistent data-driven models, so-called Lagrangian-Gaussian Processes, to identify complex nonlinear, high- or inifinite-dimensional, and coupled dynamics. We exploit energy components and the differential equation structure to consistently model these systems in an efficient manner. We account for inherent robustness in the learning as well as the control phases, and for physical intuition of the data-driven model, by making use of structurally preserving passivity-based control methods, minimally changing and exploiting the dynamics, instead of, e.g., canceling all nonlinearities to achieve linear dynamics.
Acknowledgment
This work is supported by the Consolidator Grant ”Safe data-driven control for human-centric systems” (CO-MAN) of the European Research Council (ERC) under grant agreement ID 864686.
Safe Learning-Based Control for Systems with Latent States
Researcher: Robert Lefringhausen
Motivation
Learning-based methods are frequently used to model highly complex systems. Often not all time-varying quantities that influence the system behavior (so-called states) can be directly measured. Latent states complicate learning-based system identification since both the unknown dynamics and the internal states must be jointly estimated. Assessing the model uncertainty due to finite and noisy data is challenging for systems with latent states. The quantification of uncertainty is needed to provide formal robustness guarantees, which are crucial to apply the resulting algorithms in safety-critical domains, e.g., to control robots that operate close to humans. Therefore, our research aims to develop and analyze learning-based control approaches with safety guarantees for systems with latent states.
Research questions
- How can the internal state and the dynamics of a system be jointly estimated?
- How can the uncertainty be quantified and exploited for control?
- Is it possible to guarantee the convergence of the estimation and the robustness and stability of the closed-loop system?
Approach
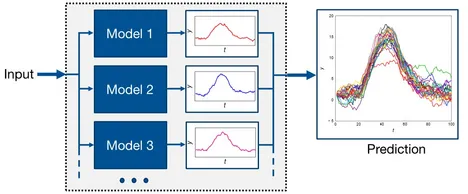
We focus on parametric approximations of Gaussian process models to describe the unknown dynamics. The uncertainty over the dynamics is expressed as uncertainty over the parameters. The distribution of the model parameters and the internal states is approximated by iterative sampling. Repeatedly, a state trajectory is sampled based on the current model, and afterward, the model is updated based on the trajectory (particle Gibbs sampling). The result are parameter samples that represent a distribution over models. Instead of a single model, we sample multiple models that can explain the observations. The models yield different outputs for a given input sequence that capture the uncertainty over a prediction (see figure).
Acknowledgment
This work is supported by the ONE Munich Strategy Forum Project “Next generation Human-Centered Robotics".