Cooperative Robotics

Cooperative robotics is the application field where the areas of networked control, data-driven control, human-centered control and bio-inspired design come together. Examples include distributed multi-agent systems and human-centered robot control. Additionally, on a physical level of interaction, we perform an exploration of haptics in cooperative control with teams of humans and robots. Employing haptic devices in cooperative control necessitates recognition and prediction of human haptic intention, as well as architectures enabling cognitive team control. On a practical side, we are also interested in employing control and motion schemes for state-of-the-art robots moving into dynamic home environments, with a human present. Such methods need to be safe for the user and robust in task execution, putting an emphasis on sound experimental validation.

Current topics:

Robotics in maximal coordinates

Researcher: Jan Brüdigam

Motivation

Typically, robotic systems are described in minimal (also called generalized) coordinates. Here, each coordinate represents a single degree of freedom of the underlying structure (for example the angle of a pendulum). The advantage of this parameterization lies in the small number of variables and the avoidance of constraints.

However, for modern robots carrying out complicated tasks, for example collaboratively carrying objects, minimal coordinates are not always ideal. Instead, it can be beneficial to use maximal coordinates resulting in a decoupled description of the system which can then be put together with additional constraints. This type of representation offers a number of numerical and control theoretic advantages. At the same time there are quite a few open questions still to be answered.

Research Questions

Variational integrators are the ideal method to numerically integrate systems in maximal coordinates, but currently, only first-order methods are used. The development of higher-order variational integrators could provide improved performance.
The modular structure of maximal coordinates is a key advantage over minimal coordinates and allows for the development of efficient parallelization and differentiation schemes.
The accurate depiction of contact interactions and friction is still a widely research topic in the area of robotics and maximal coordinates can provide several advantages for treating such scenarios.

Approach

By using (higher-order) variational integrators, we can exploit the numerical advantages of maximal coordinates while avoiding the drawback of constraint drift, a property typical for regular integration of constraints. Following graph-based algorithms and modern optimization approaches allows us to derive efficient and performant numerical algorithms even for complex scenarios.

Key Results and Achievements

Sparse factorization algorithm to solve dynamics in maximal coordinates in linear time.
First-order variational integrator for dynamics in maximal coordinates.
Code for a dynamics simulation in maximal coordinates can be found here: https://github.com/janbruedigam/ConstrainedDynamics.jl

Adaptive torque observer for human-exoskeleton interaction

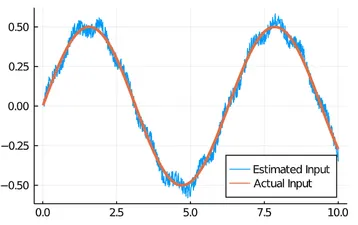
Researchers: Jan Brüdigam, Samuel Tesfazgi

Motivation

Patients having suffered accidents or stroke often have to go through extensive rehabilitation to regain motor skills for an independent and self-determined life. In contrast to classical physical therapists, robotic rehabilitation systems are able to tirelessly and precisely apply intense manual labor over long periods of time, while accurately measuring performance and improvements of the patient.

The development of upper-body shared control strategies for rehabilitation routines requires accurate estimation of the human input during human-exoskeleton interactions. The main challenges for this estimation are the human model uncertainties.

Research questions

How to efficiently incorporate passive degrees of freedom and varying connection points
How to deal with human model uncertainties

Approach

We are developing a torque observer based on the physical model of the exoskeleton and a nominal model of the human in combination with a data-driven identification of residual human model parameters to obtain precise results.