Inaktiv: Der Benutzer ist in TUMonline nicht mehr aktiv!
Inactive: The user is not active in TUMonline anymore!
Inactive: The user is not active in TUMonline anymore!
Short Biography
- 01/2021 - present: PhD candidate at Chair of Information-Oriented Control (ITR),
Technical University of Munich (TUM), Germany.
- 11/2019 - 12/2020: R&D Control Engineer,
Blickfeld GmbH, Munich, Germany.
- 10/2017 - 11/2019: M.Sc. in Electrical Engineering and Information Technology,
Technical University of Munich (TUM), Germany.- Thesis: Nonlinear Oscillations of a Laser Beam Deflection Unit with Multiple Degrees of Freedom
- Thesis: Nonlinear Oscillations of a Laser Beam Deflection Unit with Multiple Degrees of Freedom
- 10/2014 - 09/2017: B.Sc. in Electrical Engineering and Information Technology,
Technical University of Munich (TUM), Germany.- Thesis: Stochastic Newton-based Extremum Seeking with Constant Delays
Research Interests
General
- Stability-oriented learning in data-driven control for safety guarantees
- Stability analysis techniques and probablistic uncertainty-handling methods
- Nonlinear systems, soft robotics, aerodynamics
- Passivity-based control
- Gaussian processes
Motivation
Lagrangian systems comprise a large class of physical systems such as robots, aircrafts or marine vehicles. The application of Gaussian Processes (GPs) in learning-based control has the potential to significantly improve criteria such as performance and safety. However, in general GP regression does not account for key problems such as:
- physical consistency, i.e., the fulfillment of the fundamental underlying physical properties,
- the trade-off between physics-imposed symmetries and model flexibility,
- reliable and robust applicability in the control of uncertain physical/passive systems,
- computational efficiency and data-efficiency.
Approach
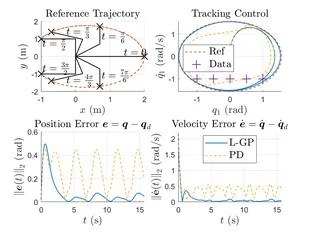
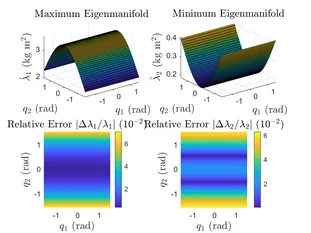
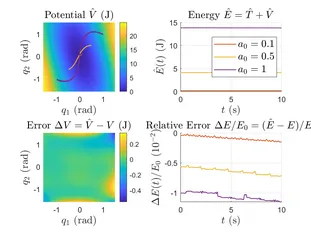
Our main approach is to construct & apply physically consistent data-driven models, so-called Lagrangian-Gaussian Processes, to identify complex nonlinear, high- or inifinite-dimensional, and coupled dynamics. We exploit energy components and the differential equation structure to consistently model these systems in an efficient manner. We account for inherent robustness in the learning as well as the control phases, and for physical intuition of the data-driven model, by making use of structurally preserving passivity-based control methods, minimally changing and exploiting the dynamics, instead of, e.g., canceling all nonlinearities to achieve linear dynamics.
Acknowledgment
This work is supported by the Consolidator Grant ”Safe data-driven control for human-centric systems” (CO-MAN) of the European Research Council (ERC) under grant agreement ID 864686.
Student Theses
I am continuously searching for motivated & excellent students who are interested in my research. In order to apply, please send me your CV and transcript of records to: g.evangelisti@tum.de
Unsolicited applications are also welcome in case no open topics are listed.
Currently available theses:
- Physically Consistent Learning & Control of Lagrangian Systems with Dissipation (PDF)