Software for current publications from our chair can be found on GitHub.
Stable Gaussian Process based Tracking Control of Lagrangian Systems
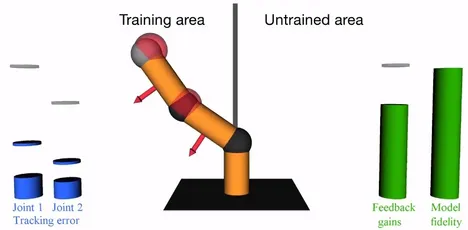
High performance tracking control can only be achieved if a good model of the dynamics is available. However, such a model is often difficult to obtain from first order physics only. In this paper, we develop a data-driven control law that ensures closed loop stability of Lagrangian systems. For this purpose, we use Gaussian Process regression for the feedforward compensation of the unknown dynamics of the system. The gains of the feedback part are adapted based on the uncertainty of the learned model. Thus, the feedback gains are kept low as long as the learned model describes the true system sufficiently precisely. We show how to select a suitable gain adaption law that incorporates the uncertainty of the model to guarantee a globally bounded tracking error. A simulation with a robot manipulator demonstrates the efficacy of the proposed control law.
The code for the publication "Stable Gaussian Process based Tracking Control of Lagrangian Systems" by Thomas Beckers, Jonas Umlauft, Dana Kulic, Sandra Hirche published at the IEEE Conference on Decision and Control (CDC) 2018 is available here.