How the inner ear works

Introduction

Our hearing organ is extremely sensitive, when we hold a shell behind our ear (or form one with our hand) we hear the "surf of the ocean", at least this is what my grandmother told me. In fact, it is the noise of the air molecules crackling on the ear drum. So the sensitivity our hearing system is limited by Brownian motion. Here are two overview publications (English and German) that describe how we think that works:

Modeling auditory coding: from sound to spikes PDF

Codierung von Schallsignalen in Aktionspotenziale des auditorischen Nervs PDF

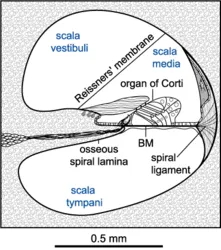
Micromechanics of the inner ear

Cochlear duct in the apical part of the inner ear

The hearing organ is a fascinating micromechanical system, which is sensitive to vibrations in the sub-nanometer range. Scan my publications from the Tübingen Hearing Research Laboratory to find out how we measured the vibration of all major components of the organ of Corti not only in one dimension but three-dimensional. For this feat I was awarded with the Helmholtz prize of the PTB (Physikalisch-Technische Bundesanstalt, the German equivalent to the National Institute of Standards).

Morioka, I., Reuter, G., Reis, P., Gummer, A.W., Hemmert, W. and Zenner, H.-P. (1995): Sound-induced displacement responses in the plane of the organ of Corti in the isolated guinea-pig cochlea. Hear. Res. 83, 142-150.
Gummer, A.W., Hemmert, W., Zenner, H.-P. (1996): Resonant tectorial-membrane motion in the inner ear: Its crucial role in frequency tuning. Proc Natl Acad Sci USA 93, 8727-8732.
Hemmert, W. (1997): Dreidimensionale Schwingungsmessungen im Innenohr: Aufklärung der Frequenzselektivität des Gehörs. PTB-Mitteilungen 107 1/97: 12-18.Hemmert, W., Zenner, H.-P. and Gummer, A.W. (2000a):Characteristics of the travelling wave in the low-frequency region of a temporal-bone preparation of the guinea-pig cochlea. Hear. Res. 142 (1-2) pp. 184-202.Hemmert, W., Zenner, H.-P. and Gummer, A.W. (2000b): Three dimensional motion of the organ of Corti. Biophys. J. 78: 2285-2297.
Freeman, D.M., Abnet, C.C., Hemmert, W., Tsai, B.S. and Weiss, T.F. (2003): Dynamic material properties of the tectorial membrane: a summary. Hear. Res. 180 pp. 1-10.

Mechanics of cochlear outer hair cells

Measurement of OHC receptor potental with a patch-clamp capillary (from the left) due to stimulation of their hair bundle (capillary from the right)

Cochlear outer hair cells (OHC) are amazing: they do not only depolarize when their hair bundle is deflected in excitatory direction, they also contract due to this depolarization.

It is thought that OHC provide active amplification of the travelling wave in the inner ear. Therefore we have studied their mechanics and their motility in detail:

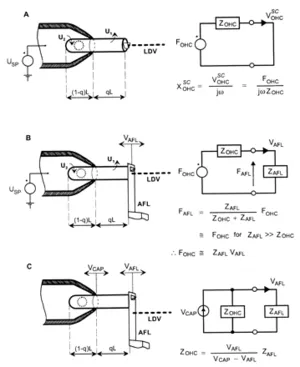
_{Experimental configurations for measuring the electromechanical properties of an isolated OHC partially inserted into a micropipette. (A) electrically induced displacement of the cuticular plate of the OHC, the so-called electromotility, xOHC. (B) The electromechanical force, FOHC, produced by the OHC under loaded conditions. (C) The mechanical impedance, ZOHC, of the OHC. Circuit diagrams are the electrical equivalents of OHC mechanics, with forces given as voltages and velocities as currents. A command voltage, USP, applied to the pipette solution induces voltage drops, U1 and U2, across those sections of the cell membrane excluded from and contained in the pipette, respectively; U1 and U2 are of opposite phase. The electromotility (A) was determined by focusing the beam of a laser Doppler vibrometer (LDV) onto the cuticular plate of the OHC. FOHC (B) was determined by placing a lever used in atomic force microscopy (AFL), against the cuticular plate. ZOHC (C) was determined by mechanically vibrating the micropipette with a piezoelectric actuator with velocity VCAP and measuring the resulting velocity of the AFL.}

Our results demonstrate the outstanding speed of outer hair cell motility. In fact, to our knowledge, they represent the fastest cellular motility ever measured.

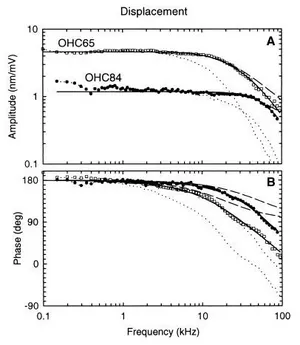
_{Displacement amplitude (A) and phase (B) of electrically induced length changes of two OHCs of different length measured under unloaded conditions. Phase is referred to a depolarizing membrane potential and is positive for contraction; that is, for displacement away from the LDV. The data (symbols) are shown corrected for the measured electrical low-pass filter characteristic of the microchamber, with the OHC attached (dotted lines). Displacement data were fitted by the amplitude and phase responses of a second-order resonant system (full lines), representing the mechanical properties of the cell and extracellular fluid}

Preyer, S., Pfister, M. und Hemmert, W. (1993): Mechanische Reizung isolierter äußerer Haarzellen als Testsystem: Hemmung der Transduktion nach Streptomyzinbehandlung. HNO 41, 471-474.
Preyer, S., Hemmert, W., Pfister, M., Zenner, H.-P. and Gummer, A.W. (1994): Frequency response of mature guinea-pig outer hair cells to stereociliary displacement. Hear. Res. 77, 116-124.
Reuter, G., Kössl, M., Hemmert, W., Preyer, S., Zimmermann, U. and Zenner, H.-P. (1994): Electromotility of outer hair cells from the cochlea of the echolocating bat, Carollia perspicillata. J. Comp. Physiol. A. 175:449-455
Preyer, S., Hemmert, W., Zenner, H.-P. and Gummer, A.W. (1995): Abolition of the receptorpotential of isolated mammalian outer hair cells by hair-bundle treatment with elastase: a test of the tip-link hypothesis. Hear. Res. 89, 187-193.
Preyer, S., Renz, S., Hemmert, W., Zenner, H.-P. and Gummer, A.W. (1996): Receptor potential of outer hair cells isolated from base to apex of the adult guinea-pig cochlea: Implications for cochlear tuning mechanisms. Auditory Neuroscience 2, 145-157.
Frank, G., Hemmert, W. and Gummer, A.W. (1997): Limiting dynamics of high-frequency electromechanical transduction of outer hair cells. Proc Natl Acad Sci USA 96, 4420-4425.

Mechanical properties of the tectorial membrane

The mammalian sense of hearing relies on a series of mechanical processes that deflect the sensory bundles of hair cells in the cochlea. Overlying these bundles is an a cellular gel called the tectorial membrane (TM), which is believed to play a critical mechanical role in cochlear function. As until recently rather little has been known about the dynamic material properties of the tectorial membrane, we have developed a number of methods to provide appropriate measurement data.

Left: Schematic diagram (not to scale) illustrating the apparatus used for the force probe method for measuring the mechanical properties of the isolated TM at audio frequencies. Right: Measurement on a TM specimen.

Mechanical impedance in the transversal direction (upper panel: magnitude, lower panel: phase) measured on 8 different locations from 6 preparations in the frequency range from 10 Hz up to 3 kHz.

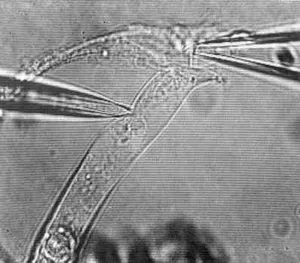
In a second approach, we designed and bulk fabricated micro-scale mechanical probes for applying shearing forces to biological tissues. We used these probes to measure shear impedance of the tectorial membrane (TM) in two dimensions.

_{Microfabricated probe on a TM specimen. The probe consisted of a base and shearing plate connected by two flexible arms. The probe was capable of applying force in the radial and longitudinal directions, indicated by the arrows in the lower left hand corner. Displacements applied to the probe base caused bending of the cantilever arms, as illustrated with dashed lines (bending is exaggerated for clarity). The radial fibrillar structure of the TM is readily visible in the image and was used to align the radial and longitudinal axes, the radial axis being parallel to the radial fibrils.}

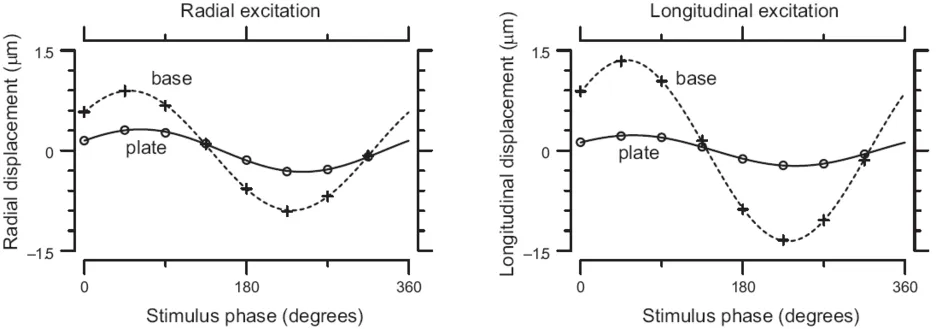
Typical motions of probe on TM over one stimulus cycle. Description see below.

_{Typical motions of probe on TM over one stimulus cycle. The left plot shows radial displacement over one stimulus cycle for radial excitation, and the right one shows longitudinal displacement for longitudinal excitation. The motions of the base (plusses) and plate (circles) were approximated by sinusoidal functions (dashed and solid curves). The amplitude of motion of the plate, which contacted the TM, was smaller than that of the base. These measurements were for TM preparation 3 at stimulus frequency 100 Hz.}

TM impedance versus frequency. Description see below.

_{TM impedance versus frequency. The magnitude (top) and phase (bottom) of TM shear impedance are plotted vs. frequency for both radial (left) and longitudinal (right) forces. Different symbol types represent individual TMs. The lines represent least-squares power-law fits to measurements from individual TMs. The slopes of these power-law relations were −16 ± 0.4 dB/decade and −19 ±0.4 dB/decade for radial and longitudinal forces, respectively. The dotted and dashed lines represent the frequency response of a pure elastic spring (slope −20 dB/decade and phase −90°) and a pure viscous damper (slope 0 and phase 0°), respectively.}

Our results show that the viscoelastic properties of the TM extend over a significant range of audio frequencies, consistent with a poroelastic interpretation of TM mechanics. The shear modulus G′ determined from these measurements was 17–50 kPa, which is larger than in species with a lower auditory frequency range. This value suggests that hair bundles cannot globally shear the TM, but most likely cause bulk TM motion.